Was sind Neuronale Netze und wie funktionieren sie?

Nimmt man es ganz genau, haben wir es auch hier nicht mit einer “Erfindung” der letzten Jahre zu tun, sondern mit einer Technik, die schon vor Jahrzehnten “erdacht” wurde, durch technologische Neuerungen (Rechenleistung, Verfügbarkeit von Daten u.ä.) aber erst vor rund 15 Jahren Fahrt aufnahm. Das aber nur am Rande, denn um das Thema “Neuronale Netze” ranken sich so viele Missverständnisse und Irrtümer, dass wir ihnen einen eigenen Beitrag widmen werden.

Was sind Neuronale Netze?

Was meinen wir aber, wenn wir von “Neuronalen Netzen” sprechen? Ganz formell spricht man eigentlich von „Künstlichen Neuronalen Netzen“ (KNN) oder auf Englisch auch „Artificial Neural Networks“ (ANN), denn: „Richtige“ neuronale Netze finden sich nur in höheren Lebewesen, nicht in Software oder Maschinen. In der Welt der IT werden die Begriffe aber wild durcheinander benutzt und bezeichnen alle in der Regel immer künstliche neuronale Netze. Meint man explizit „echte“ neuronale Netze in Lebewesen, spricht man dann oft der Klarheit halber von biologischen Neuronalen Netzen.

Neuerdings wird oft nicht mehr von Neuronalen Netzen, sondern von Deep Learning gesprochen. Das kommt daher, dass es die neuesten, tollen Ergebnisse nur dann erreicht werden, wenn man Neuronale Netze aus mehreren Schichten aufbaut, sie also „tief“ sind. Wenn man es also ganz genau nimmt, heißt Deep Learning „maschinelles Lernen mit künstlichen neuronalen Netzen aus mehreren Schichten“. Aber auch hier werden die Begriffe heutzutage synonym verwendet: Alle interessanten Neuronalen Netze sind ohnehin „tief“, so dass KNN und DL in der Praxis eigentlich das gleiche bezeichnen.

Künstliche neuronale Netze – Aufbau & Funktionsweise

Es gibt sehr viele verschiedene Arten von neuronalen Netzen (auch Architekturen genannt). Um eine Aufgabe zu lösen ist es oft sehr wichtig, genau die richtige Herangehensweise zu wählen. Oft bestehen komplexe Architekturen aus mehreren einfacheren Netzen, die dann auf die richtige Art und Weise kombiniert werden. Im Gegensatz zu unserem Gehirn, dass sich dynamisch blitzschnell an viele Aufgaben anpassen kann, sorgen schon kleinste Fehler dafür, das ein Neuronales Netz versagt und gar nichts lernt. Wählt man die falsche Architektur für eine Aufgabe, hat man meist keine Chance mehr auf gute Resultate.

Jede Architektur funktioniert natürlich anders, aber alle Neuronalen Netze haben dieselbe grundlegende Funktionsweise, die man am besten mit dem Klassiker unter den Neuronalen Netzen erläutert, dem „fully connected neural Network“ oder auch „feed-forward neural network“, manchmal auch etwas ungenau Multi-Layer-Perceptron genannt.

Die Funktionsweise des “Fully Connected Neural Network”

Die meisten anderen Beschreibungen von Neuronalen Netzen fangen nun mit einer biologisch nicht akkuraten Beschreibung von Neuronalen Netzen an und versuchen daran zu erklären, wie KNN in Computern funktionieren. Leider hinkt dieser Vergleich stark und birgt die große Gefahr, ein falsches Gefühl dieser Technik zu entwickeln. Daher lassen wir die biologische Inspiration außen vor und fangen gleich mit einem echten KNN an.

Ein KNN besteht in der Regel aus mehreren Schichten. Eine Schicht bekommt als Eingabe eine (manchmal sehr große) Zahlenkolonne (Vektor) und erzeugt eine neue Zahlenkolonne, die nur auf dieser Eingabe beruht. Diese neue Zahlenkolonne kann kürzer, länger oder gleich groß sein. Dabei führt jede Schicht meist nur sehr wenige Rechenoperation auf den Eingabezahlen aus (z.B. eine Multiplikation oder Addition).

Um eine Vorstellung zu bekommen, wie eine Schicht eines echten Künstlichen Neuronalen Netzes arbeitet, schauen wir uns nun das Fully Connected Neural Network an.

Die drei Schritte des “Fully Connected Neural Network”

Beim Fully Connected Neural Network folgen zum Beispiel nur drei Schritte abwechselnd immer wieder aufeinander:

1. Multiplikation mit Konstanten und Addition der Ergebnisse

2. Addition von Konstanten

3. und eine sogenannte Aktivierungsfunktion.

Alle drei Schritte hintereinander nennt man ein „Schicht“ des neuronalen Netzes. In jeder Schicht sind zusätzlich eine Menge von Zahlen abgespeichert, oft werden diese Zahlen „Gewichte“ genannt. Interessanterweise ist die Mathematik, mit der ein neuronales Netz seine Ergebnisse berechnet, enorm einfach. Eigentlich reicht dazu sogar Grundschulwissen.

Fangen wir an mit Schritt 1. Um einen einzigen Ausgabewert zu berechnen, wird jeder Eingabewert mit einer der in der Schicht gespeicherten Zahlen multipliziert. Die Ergebnisse dieser Multiplikationen werden aufaddiert. Wie oft das gemacht wird, hängt davon ab, wie viele neue Werte man möchte.
Nehmen wir an, wir möchten eine Schicht, in die man 768 Werte herein schicken und von der man 512 Resultate erhalten kann. Dann wird dieser Prozess 512-mal (für jede gewünschte Ausgabe) mit allen 768 Eingaben wiederholt, jedes mal mit anderen in der Schicht gespeicherten Zahlen. Das Netz muss in der Schicht für diesen Schritt also 512*768=393.216 Zahlen vorhalten.

Schritt 2 ist noch einfacher: Auf jedes Ergebnis des vorigen Schritts wird eine weitere, im Neuronalen Netz gespeicherte Zahl aufaddiert. Für diesen Schritt braucht es in unserem Beispiel also 512 weitere Zahlen in einer Schicht.

Schritt 3 wird sogar noch einfacher: Hierbei werden wieder die vorigen Ergebnisse genommen. Diesmal wird nur geschaut, ob das Ergebnis größer ist als null, wir brauchen also keine gespeicherten Zahlen aus dem Netz. Ist das Ergebnis größer als null, wird es einfach weitergeleitet. Ist es kleiner null, wird es durch null ersetzt. Das ist die Aktivierungsfunktion. Eindrucksvoller Name, wenig dahinter.

“Lernen” durch Wiederholung und Verbesserung

Dieser Drei-Schritte-Prozess des Fully Connected Neural Networks wird immer wieder wiederholt, bis alle Schichten des KNN durchlaufen sind. Aber wo kommen diese Zahlen her, mit denen multipliziert und addiert wird?

Im Gegensatz zur Struktur des Netzes (die Anzahl der Schichten, die Anzahl der Ein- und Ausgabewerte), sind diese nicht durch seine Programmierung definiert. Stattdessen werden sie initial mit Zufallszahlen belegt. Das bedeutet: ein frisch geschlüpftes neuronales Netz produziert nur Unsinn aus seiner Eingabe, indem es wild mit Zufallszahlen multipliziert und addiert.

Jetzt kommt das berüchtigte „Lernen“ ins Spiel. Dieses funktioniert genau wie in unserem Blogartikel “Die Grundlagen des Machine Learning” erläutert. Immer, wenn ein Neuronales Netz etwas lernen soll, braucht es eine Reihe von Eingaben, zusammen mit dem zu erzeugenden Ergebnis. Der beste Testdatensatz für Neuronale Netze ist hier der sogenannte MNIST-Datensatz. Hierbei handelt es sich um tausende schwarz-weißer Bilder von handgeschriebenen, einzelnen Ziffern (0 bis 9).

Für jedes Bild ist bekannt, welche Ziffer darauf zu sehen ist. Die Bilder sind 28 mal 28 Pixel groß. Das neuronale Netz braucht alle Pixel zur Berechnung eines Ergebnisses, die erste Schicht muss also groß genug für 28*28=768 Eingaben sein.

Praxis-Beispiel eines Fully Connected Neural Networks

Wenn wir nun ein Fully Connected Neural Network darauf „trainieren“ wollen, einem Bild die richtige Ziffer zuzuordnen (sie, vermenschlicht gesagt, zu “erkennen”), müssen wir es zunächst sinnvoll aufsetzen. Stimmt das Set-Up, wird das Neuronale Netz sich nach und nach über die immer weiter bereinigten Abweichungen an das richtige Zuordnen der Bilder herantasten.

Das Neuronale Netz als Bilderkenner: Setup

I. Der Input bekommt so viele Werte, wie Pixel in einem der MNIS-Ziffern-Bilder sind (28*28=784). Wir geben also jedesmal alle Pixel auf einmal in das Neuronale Netz.

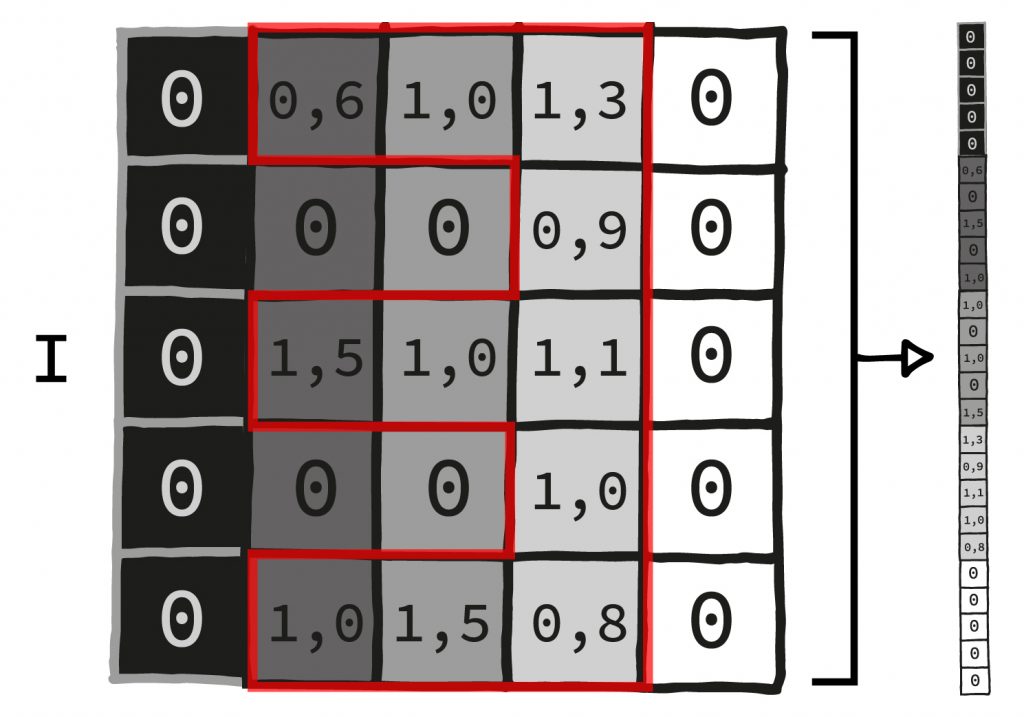
II. Nun schichten wir ca. fünf Schichten wie oben beschrieben aufeinander, also fünf mal die Schritte Multiplikation und Addition, Addition und Aktivierungsfunktion. Dabei ist die Ausgabe jeder Schicht immer kleiner als ihre Eingabe. (Das muss nicht bei jedem neuronalen Netz so sein, in diesem Fall funktioniert es aber gut).

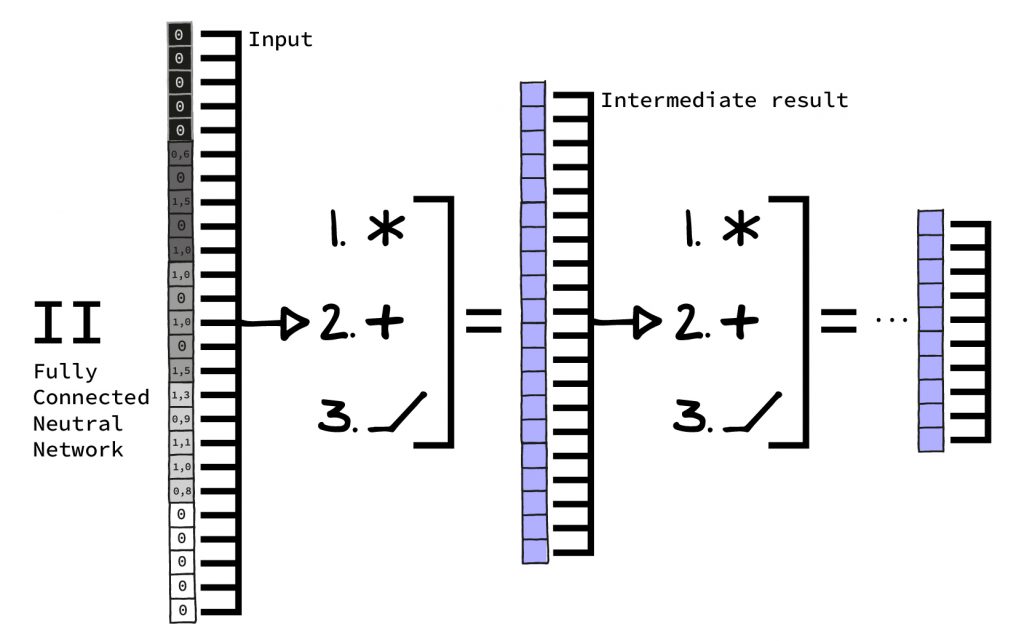
III. Die letzte Schicht hat 10 Ausgabewerte, einen Wert für jede mögliche Ziffer, die es zu erkennen gilt. Dabei steht jeder Wert dafür, für wie ähnlich das Netz die Eingabe zu einer Ziffer hält. Hier sieht man sehr schön die „ungenaue“ Rechenweise eines Neuronalen Netzes. Es gibt nicht eine Ziffer aus, sondern benennt die Wahrscheinlichkeit für jedes Ergebnis. In der Praxis wählt man meist einfach die Antwort mit der höchsten Wahrscheinlichkeit, wenn man eine einzige Antwort möchte.

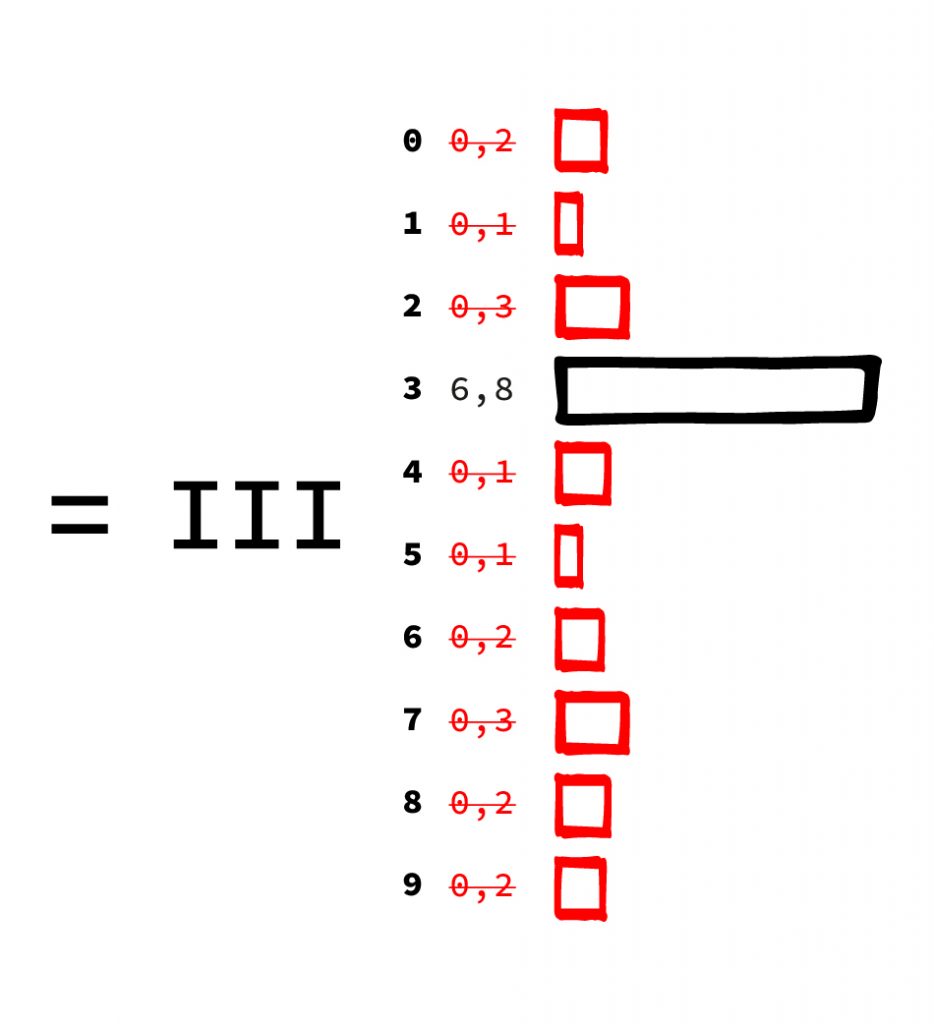
Bevor wir das Netz trainieren können, werden die ganzen Zahlen, die in jeder Schicht verwendet werden, mit Zufallszahlen gefüllt. Das klingt erstmal sinnlos, hat aber einen ganz praktischen Grund: Wir wissen ja nicht, wie das Netz die Aufgabe lösen soll – das soll es im nächsten Schritt selber lernen. Da wir selber keine Ahnung haben, wählen wir den Startpunkt des Lernvorgangs durch Zufallszahlen zufällig.

Training und “Backpropagation”

Nun haben wir den Aufbau des Netzes definiert. Man könnte das KNN nun sogar schon starten, allerdings wäre dies ziemlich nutzlos: Durch die Initialisierung mit Zufallszahlen ist das Ergebnis zunächst komplett wertlos. Dies ändert sich erst mit dem nächsten Schritt – dem Training.

Wir nehmen hierzu einen Teil der MNIST-Bilder (ca. 90%) und geben sie nacheinander in das Neuronale Netz. Dann schauen wir uns an, was herauskommt. Diesen Schritt nennt man auf Forward Pass, die Bilder laufen vorwärts durch das Netz. Wir vergleichen die zehn Ausgabewerte mit dem tatsächlichen Ergebnis. Für ein Bild mit einer 3 wäre das gewünschte, perfekte Ergebnis ja [0: 0%, 1: 0% , 2: 0%, 3: 100%, 4: 0%, 5: 0% … ]. Wir können nun durch einfaches Subtrahieren ausrechnen, wie falsch das Neuronale Netz für jeden Prozentwert liegt. Diese numerische Angabe der „Falschheit“ ist der Trick beim Trainieren von Neuronalen Netzen.

Der berechnete Fehler wird benutzt, um mit einem speziellen Algorithmus namens „Backpropagation“ die im neuronalen Netz gespeicherten Konstanten so zu ändern, dass das Ergebnis ein wenig besser wird. Dazu wird der Fehler über alle Schichten „aufgeteilt“ und die ganzen Konstanten werden ein klein wenig auf- oder abjustiert. Der Algorithmus bestimmt also mathematisch, welcher Teil des Netzes den schwersten Fehler verursacht hat und entsprechend gewichtet durch das Justieren “gegensteuern”. Dies ist der sogenannte Backward Pass, weil der Fehler rückwärts (von der Ausgabe zur Eingabe) durch das Netz fließt.

Beim nächsten Mal liegt das Netz dann etwas weniger daneben und das Ergebnis wird wiederholt. Das muss man eine ganze Weile machen. Bei einfachen Problemen wie den MNIST Bildern einige zehn- oder hundertausendmal. Bei schweren Problemen wie der Fußgängererkennung für ein selbstfahrendes Auto auch gerne einmal einige Milliarden Male. Man sieht hier sehr schön einen deutlichen qualitativen Unterschied zu unserem Gehirn: Der Mensch braucht viel, viel weniger Beispiele, um eine Aufgabe zu lernen.

Überprüfung des Trainings anhand der Testdaten

Ist der Fehler beim Training klein genug, hört man mit dem Trainieren auf. Dann kommen die letzten 10% der Daten (Testdaten) ins Spiel, die wir bisher nicht zum Training genutzt haben. Diese hat das Netz ja noch nie gesehen und konnte sie deshalb nicht „auswendig lernen“. Hiermit überprüfen wir, ob das Netz nun wirklich Ziffern erkennen kann. Ist das Netz in der Lage, auf eine für uns akzeptablen Menge von Bildern die richtige Antwort zu liefern, haben wir erfolgreich unser erstes Neuronales Netz trainiert.
Liegt es auf diesem sogenannten Test-Set gründlich daneben, obwohl der Fehler beim Training schön niedrig war, haben wir sogenanntes „Overfitting“. Das Netz hat nicht zu abstrahieren gelernt, sondern nur die Trainingsbilder auswendig gelernt. Wir haben irgendwo einen Fehler gemacht und müssen wieder von vorne anfangen.